KG场的路径积分

路径积分的思想为：所有可能的路径都对传播子有贡献，权重为作用量的指数因子。其优势有

能自然地给出编时乘积的期望值
所有量都是纯数/Grassmann数，无需考虑复杂的算符对易关系
只需求导，计算方便~~代价是最开始的计算复杂~~
数值计算方便、误差小~~可能吧，别人说的，我也不知道~~

在应用到四维时空上时出现了很严重的问题，希望将来能够解决。

[ ] 在欧氏空间和闵氏空间里分别计算传播子

路径积分与编时算符期望值

约定 $t_\pm$ 满足 $\Im(t_\pm)\rightarrow\mp\infty$，实部不做限制。假设Hamiltonian最低本征值为0，则对于任意态矢，只要和基态不正交，就有

$e^{iHt_-}|1\rangle=\langle0|1\rangle|0\rangle,\langle2|e^{-iHt_+}=\langle0|\langle2|0\rangle$

所以海森堡表象中

$\langle0|Q(t_1)Q(t_2)|0\rangle=\frac{\langle2| e^{-iH(t_+-t_1)}Q(0)e^{-iH(t_1-t_2)}Q(0)e^{-iH(t_2-t_-)}|1\rangle}{\langle2|e^{-iH(t_+-t_-)}|1\rangle}\tag{1}$

用$Q$的本征值构造恒等算符，在$Q(0)$附近插入

取足够多的“时间”点使得对于$j=0\sim N,t^{(j)}-t^{(j+1)}\rightarrow0+0i$，右边强调的是虚部和实部都足够“连续”。其中$|q^{(0)}\rangle=|2\rangle,|q^{(N+1)}\rangle=|1\rangle,t^{(i_1)}=t_1,t^{(i_2)}=t_2$。(1)式变为

$分子=\int\prod_{j=1}^N\left(\mathrm dq^{(j)}\right)q^{(i_1)}q^{(i_2)}\prod_{j=0}^N\langle q^{(j)}|e^{-iH(t^{(j)}-t^{(j+1)})}|q^{(j+1)}\rangle$

第二个连乘中每一项都插入正则动量$P$的完备性关系，考虑到$\delta t$保留一阶项时总误差能控制在一阶，所以指数上的算符可以“当作纯数”来处理

$\prod_{j=0}^N\int\frac{\mathrm d^dp}{(2\pi)^d}e^{-iH(p,q)\delta t}e^{ip(q^{(j)}-q^{(j+1)})}=\exp\left[i\int_{t_-}^{t_+}\mathrm dt\ \left(p\dot q-H\right)\right]$

指数上为作用量$iS=i\int L\mathrm dt$。同样可以计算(1)的分母，所以完整形式为

$\langle 0|Q(t_1)Q(t_2)|0\rangle=\frac {\int[\mathrm dq]\ q(t_1)q(t_2)e^{iS}} {\int[\mathrm dq]\ e^{iS}}\tag{2}$

常见路径（编时、虚时）

当然可以额外要求$\Im\left(t^{(j)}-t^{(j+1)}\right)\le 0$，这样使得积分路径单调“下降”。如下图$\color{blue}蓝线$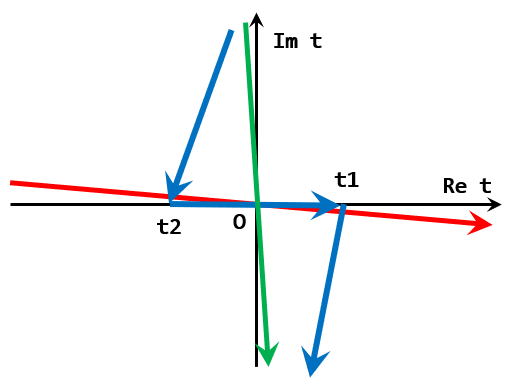

或者给时间一个很小的虚部，如$\color{red}{红线}$。此时可以看到取（几乎）实轴为路径时自动给出编时算符期望值。
在红线基础上做Wick转动，可以证明无穷远处的积分为零，所以$\color{green}{绿线}$（虚轴）积分值与红线相等。进一步可做变量代换$x^4\equiv x_4\equiv ix_0=it$，此时$\int_{green}\mathrm dt=i\int_{-\infty}^\infty\mathrm dx^4$，因此变为欧氏空间的积分。

含源路径积分和Wick定理

定义

$Z[J]=\int[\mathrm dq]\ e^{iS+\int\mathrm dt\ J(t)q(t)}\tag{3}$

则(2)式为

$\langle0|Q(t_1)Q(t_2)|0\rangle=\frac{1}{Z[0]}\left.\frac{\delta^2 Z[J]}{\delta J(t_1)\delta J(t_2)}\right|_{J=0}\tag4$

若$S$为二次型，即找得到$K(t_i,t_j)=K(t_j,t_i)$满足

$iS=-\int\mathrm dt_i\mathrm dt_j\ K(t_i,t_j)q(t_i)q(t_j)$

那么(3)式做shift：$q(t_i)\rightarrow q(t_i)+\frac12\int\mathrm dt_j\ K^{-1}(t_i,t_j)q(t_j)$可得

$Z[J]=Z[0]\exp\left[\frac14\int\mathrm dt_i\mathrm dt_j\ K^{-1}(t_i,t_j)J(t_i)J(t_j)\right]\tag5$

由(4)(5)即可很容易看出Wick定理，即高阶项可以用二阶项表示。对于有相互作用体系，作用量不再是二次型，但是可以通过微扰展开（费曼图方法）。

因此，很基础的问题是：二阶项/传播子/格林函数是什么样子的？

传播子

传播子的定义为

$\Delta(x-y)=i\langle0|T\phi(x)\phi(y)|0\rangle$

根据之前讨论，为绿线上的路径积分。KG场的作用量为

$S=\int\mathrm d^4x\ \mathcal L,\quad \mathcal L(x)=-\frac12\partial_\mu\phi(x)\partial^\mu\phi(x)-\frac12m^2\phi(x)^2$

Wick转动至虚时

做Wick转动并引入虚时$x_E^4=it,\varphi(x_E)=\phi(x)$

$iS=-\int\mathrm d^4x_E\ \frac12\left(\sum_{i=1}^4(\partial_i\varphi(x_E))^2+m^2\varphi(x_E)^2\right)$

下标$E$表示欧氏空间。做傅里叶变换

$\tilde\varphi(k_E)=\int\mathrm d^4x_E\ e^{-ik_E\cdot x_E}\varphi(x_E)$

则作用量变为

$iS=-\int\frac{\mathrm d^4k_E}{(2\pi)^4}\ \frac12\left(k_E^2+m^2\right)\tilde\varphi(k_E)\tilde\varphi(-k_E)$

根据(5)有

$Z[J(k_E)]=Z[0]\exp\left[\int\mathrm d^4 k_E\ \frac14\frac{2(2\pi)^4}{k_E^2+m^2}J(k_E)J(-k_E)\right]$

所以

$\langle0|\tilde\varphi(k_E)\tilde\varphi(l_E)|0\rangle=\frac{(2\pi)^4}{k_E^2+m^2}\delta(k_E+J_E)$

进而可计算

$\begin{aligned} \Delta_E(x_E-y_E)=&i\int\frac{\mathrm d^4k_E}{(2\pi)^4}\frac{\mathrm d^4l_E}{(2\pi)^4}\ e^{ik_E\cdot x_E+il_E\cdot y_E}\langle0|\tilde\varphi(k_E)\tilde\varphi(l_E)|0\rangle\\ =&i\int\frac{\mathrm d^4k_E}{(2\pi)^4}\frac{e^{ik_E\cdot(x_E-y_E)}}{k_E^2+m^2} \end{aligned}\tag6$

为了看得更清楚，将(6)拆分开

$\Delta(t,\mathbf x)=\Delta_E(x_E)=i\int\frac{\mathrm d^3\mathbf k}{(2\pi)^3}\int_{-\infty}^\infty\frac{\mathrm dk^4}{2\pi}\frac{e^{i\mathbf{k\cdot x}}e^{ik^4(it)}}{(k^4)^2+\mathbf k^2+m^2}$

要使$k^0$从$+i\infty\rightarrow-i\infty$，应当为$k^4=ik^0$，因此

$\Delta(t,\mathbf x)=-\int\frac{\mathrm d^3\mathbf k}{(2\pi)^3}\int_{i\infty}^{-i\infty}\frac{\mathrm dk^0}{2\pi}\frac{e^{i\mathbf{k\cdot x}}e^{-ik^0t}}{-(k^0)^2+\mathbf k^2+m^2}$

$k^0$转动回（接近）实轴，则为了不穿过极点$\pm\sqrt{\mathbf k^2+m^2}$，需要将极点写为$\pm(\sqrt{\mathbf k^2+m^2}-i\epsilon)$——也可理解为换一个实轴

$\Delta(t,\mathbf x)=-\int\frac{\mathrm d^4k}{(2\pi)^4}\frac{e^{i\mathbf{k\cdot x}}e^{-ik^0t}}{k^2+m^2-i\epsilon}\tag7$

Wick转动回实时

需要注意的是(7)式中$\Re(t)=0$，通过解析延拓至实轴可知

$\Delta(x)=-\int\frac{\mathrm d^4k}{(2\pi)^4}\frac{e^{i\mathbf{k\cdot x}}e^{-ik^0t}}{k^2+m^2-i\epsilon}=-\int\frac{\mathrm d^4k}{(2\pi)^4}\frac{e^{ik\cdot x}}{k^2+m^2-i\epsilon}\tag8$

四维时空下的传播子（有很大问题）

对于四维时空，是可以精确求出，我们从(6)和(8)分别计算之。两种方法都出现了很严重的问题，甚至比两者结果不同更加严重

欧氏空间-解析延拓

$\begin{aligned} &\Delta_E(x_E)=i\int\frac{d^4k_E}{(2\pi)^4}\frac{e^{ik_E\cdot x_E}}{k_E^2+m^2}\\ =&i\int_0^\infty\frac{k^3\mathrm dk}{(2\pi)^4}\frac{1}{k^2+m^2}\int_0^\pi\sin^2\alpha e^{ik|x_E|\cos\alpha}\mathrm d\alpha\int_0^\pi\sin\beta\mathrm d\beta\int_0^{2\pi}\mathrm d\gamma\\ =&i\int_0^\infty\frac{k^3\mathrm dk}{(2\pi)^2}\frac{1}{k^2+m^2}\frac{J_1(k|x_E|)}{k|x_E|}=\frac{im}{(2\pi)^2}\frac{K_1(m|x_E|)}{|x_E|} \end{aligned}$ $\Rightarrow\Delta(x)=\frac{im}{(2\pi)^2}\frac{K_1(m\sqrt{\mathbf x^2-t^2})}{\sqrt{\mathbf x^2-t^2}}\tag9$

它的问题在于，类空的时候有意义，类时的意义需要进一步探讨。

闵氏空间-直接计算

先对$k^0$积分：$t<0$时取上半围道，否则取下半围道

$\begin{aligned} \Delta(x)&=\int\frac{\mathrm d^3\mathbf k}{(2\pi)^4}e^{i\mathbf {k\cdot x}}\int\mathrm dk^0\frac{e^{-ik^0t}}{(k^0-\omega_{\mathbf k}+i\epsilon)(k^0+\omega_{\mathbf k}-i\epsilon)}\\ &=\int\frac{\mathrm d^3\mathbf k}{(2\pi)^4}e^{i\mathbf {k\cdot x}}\left[-\frac{\pi i}{\omega_\mathbf k-i\epsilon}\theta(t)+\frac{\pi i}{-\omega_\mathbf k+i\epsilon}\theta(-t)\right]\\ &=-i\pi\int\frac{\mathrm d^3\mathbf k}{(2\pi)^4}\frac{e^{i\mathbf {k\cdot x}}}{\omega_\mathbf k-i\epsilon}\\ &=-i\int_0^\infty\frac{k^2\mathrm dk}{(2\pi)^2}\frac{1}{\sqrt{k^2+m^2}-i\epsilon}\frac{\sin k|\mathbf x|}{k|\mathbf x|}\\ &=-\frac i{|\mathbf x|}\int_0^\infty\frac{\mathrm dk}{(2\pi)^2}\frac{k\sin k|\mathbf x|}{\sqrt{k^2+m^2}}\\ &=-\frac i{\mathbf x^2}\int_0^\infty\frac{\mathrm du}{(2\pi)^2}\frac{u\sin u}{\sqrt{u^2+m^2\mathbf x^2}}\\ \end{aligned}$

之所以能扔掉$\epsilon$，是因为即使是一阶项在$\epsilon\rightarrow0$时也趋于零。最后一个等号为变量代换。
可惜最后的积分不收敛。