量子场论对称性

本文在路径积分框架下讨论Dyson-Schwinger方程和Ward-Takahashi恒等式，以及其部分应用。

Dyson-Schwinger方程

一般形式

假设作用量为$S=S[\varphi_1(x),\varphi_2(x),\cdots,\varphi_N(x)]$，做微小平移$\varphi_a(x)\rightarrow\varphi_a(x)+\eta_a(x)$，应当有

$$\int\mathrm D\varphi\ e^{iS[\varphi]}\varphi_{a_1}(x_1)\cdots\varphi_{a_n}(x_n)=\int\mathrm D[\varphi+\eta]\ e^{iS[\varphi+\eta]}[\varphi_{a_1}(x_1)+\eta_{a_1}(x_1)]\cdots[\varphi_{a_n}(x_n)+\eta_{a_n}(x_n)]$$

其中$a_1,a_2,\cdots a_n$可以重复。由于$\eta$可以任取，选定$\eta_a\neq0$，其他均为零，保留一阶项

$$\int\mathrm D\varphi\ e^{iS[\varphi]}\left[\left(\int i\frac{\delta S}{\delta\varphi_a(x)}\eta_a(x)\mathrm dx\right)\varphi_{a_1}(x_1)\cdots\varphi_{a_n}(x_n)+\sum_{j=1}^n\varphi_{a_1}(x_1)\cdots\delta_{aa_j}\eta_a(x_j)\cdots\varphi_{a_n}(x_n)\right]=0$$

这意味着

$$i\left\langle T\frac{\delta S}{\delta\varphi_a(x)}\varphi_{a_1}(x_1)\cdots\varphi_{a_n}(x_n)\right\rangle+\sum_{j=1}^n\left\langle T\varphi_{a_1}(x_1)\cdots\delta_{aa_j}\delta^4(x-x_j)\cdots\varphi_{a_n}(x_n)\right\rangle=0\tag{1.1}$$

利用$S=\int\mathrm d^4x\ \mathcal L(\varphi,\partial_\mu\varphi)$可得

$$\frac{\delta S}{\delta\varphi_a(x)}=\frac{\partial\mathcal L}{\partial\varphi_a(x)}-\partial_\mu\frac{\partial\mathcal L}{\partial(\partial_\mu\varphi_a(x))}\tag{1.2}$$

所以Dyson-Schwinger方程为(1.1)(1.2)

例子：标量场

$$\mathcal L=-\frac12\partial_\mu\varphi\partial^\mu\varphi-\frac12m^2\varphi^2+\frac{g}{4!}\varphi^4$$

因此

$$\frac{\delta S}{\delta\varphi(x)}=-m^2\varphi+\frac{g}{3!}\varphi^3+\partial^2\varphi$$

当$n=0,1,2$时，(1.1)变为

$$\left\{\begin{aligned} &(\partial^2-m^2)\langle\varphi(x)\rangle+\frac g6\langle\varphi^3(x)\rangle=0\\ &(\partial^2-m^2)\langle T\varphi(x)\varphi(y)\rangle+\frac g6\langle T\varphi^3(x)\varphi(y)\rangle=i\delta^4(x-y)\\ &(\partial^2-m^2)\langle T\varphi(x)\varphi(y)\varphi(z)\rangle+\frac g6\langle T\varphi^3(x)\varphi(y)\varphi(z)\rangle=i\left[\delta^4(x-y)+\delta^4(x-z)\right]\langle\varphi(x)\rangle \end{aligned}\right.$$

$n=0,2$时左右都为零，显然成立。$n=1$时，按耦合系数展开，应该有

$$\begin{aligned} (\partial^2-m^2)&\Delta(x-y)=i\delta^4(x-y)\\ (\partial^2-m^2)&\int\mathrm{id}^4z\ \Delta(x-z)\Delta(z-y)\Delta(z-z)=0\\ (\partial^2-m^2)&\int\mathrm{id}^4z_1\mathrm{id}^4z_2\left[\Delta(x-z_1)\Delta(z_1-z_2)\Delta(z_2-y)\Delta^2(0)+\right.\\ &\left.\frac16\Delta(x-z_1)\Delta^3(z_1-z_2)\Delta(z_2-y)+\frac12\Delta(x-z_1)\Delta(z_1-y)\Delta(z_1-z_2)^2\Delta(0)\right]\\ &+\frac 16\int\mathrm{id}^4z\ \Delta^3(x-z)\Delta(z-y)=0 \end{aligned}$$

第一项根据$\Delta(x)=\int\frac{-i\mathrm{id}^4k}{(2\pi)^4}\frac{e^{ikx}}{k^2+m^2-i\epsilon}$即可得到。第二项利用$\Delta(0)\equiv0$的重整化方案可证。第三项由以上分析化为

$$\int\mathrm{id}^4z_1\mathrm{id}^4z_2\ \frac16i\delta^4(x-z_1)\Delta^3(z_1-z_2)\Delta(z_2-y)+\frac16\int\cdots=0$$

因此也成立。更高阶的不再验证

例子：QED

$$\mathcal L=-\bar\psi(\partial\!\!\!\backslash+m)\psi-\frac14 F_{\mu\nu}F^{\mu\nu}+ieA_\mu\bar\psi C^\mu\psi$$

因此

$$\begin{aligned} &\frac{\delta S}{\delta\psi_a(x)}=-\bar\psi_am+ieA_\mu\bar\psi_a C^\mu-\partial_\mu(\bar\psi_a C^\mu)=-[C^\mu(\partial_\mu-ieA_\mu)+m]\bar\psi_a(x)\\ &\frac{\delta S}{\delta\bar\psi_a(x)}=-(\partial\!\!\!\backslash+m-ieA_\mu C^\mu)\psi_a(x)-[C^\mu(\partial_\mu-ieA_\mu)+m]\psi_a(x)\\ &\frac{\delta S}{\delta A_\mu(x)}=ie\bar\psi C^\mu\psi-\partial_\nu F^{\mu\nu}(x) \end{aligned}$$

Ward-Takahashi 恒等式

一般情况

假设存在某个对称操作$\varphi(x)\rightarrow\varphi(x)+\delta\varphi(x)$，对应Nother流$j^\mu(x)=\delta\varphi_a(x)\frac{\partial\mathcal L}{\partial(\partial_\mu\varphi_a(x))}-K^\mu(x)$

(1.1)左乘$\delta\varphi_a(x)$并求和得

$$-i\partial_\mu\left\langle Tj^\mu(x)\varphi_{a_1}(x_1)\cdots\varphi_{a_n}(x_n)\right\rangle+\sum_{j=1}^n\delta^4(x-x_j)\left\langle T\varphi_{a_1}(x_1)\cdots\delta\varphi_{a_j}(x_j)\cdots\varphi_{a_n}(x_n)\right\rangle=0\tag{2.1}$$

QED中的应用

U(1)对称性下

$$\psi(x)\rightarrow e^{-ie\epsilon}\psi(x),\bar\psi(x)\rightarrow e^{+ie\epsilon}\bar\psi(x)$$

所以

$$\delta\psi(x)=-ie\psi(x),\delta\bar\psi(x)=+ie\psi(x),j^\mu=\sum_a(-ie\psi_a)(\bar\psi_aC^\mu)=ie\bar\psi C^\mu\psi$$

$n=2$时

$$-i\partial_\mu\langle Tj^\mu(x)\psi_a(y)\bar\psi_b(z)\rangle+\delta^4(x-y)\langle T\delta\psi_a(y)\bar\psi_b(z)\rangle+\delta^4(x-z)\langle T\psi_a(y)\delta\bar\psi_b(z)\rangle=0$$

即为

$$-i\partial_\mu\langle Tj^\mu(x)\psi_a(y)\bar\psi_b(z)\rangle+ie\left[-\delta^4(x-y)+\delta^4(x-z)\right]\langle T\psi_a(y)\bar\psi_b(z)\rangle=0$$

第一项绘图为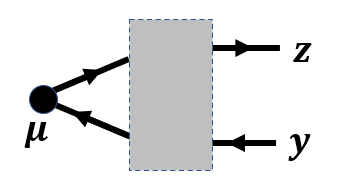

做Fourier变换

$$k_\mu\langle j^\mu(k)\psi_a(k_y)\bar\psi_b(k_z)\rangle-ie\langle\psi_a(k+k_y)\bar\psi_b(k_z)\rangle+ie\langle\psi_a(k_y)\bar\psi_b(k_z-k)\rangle=0$$

因此$k+k_y=k_z$，所以

$$(k_2-k_1)_\mu\langle j^\mu(k_2-k_1)\psi_a(k_1)\bar\psi_b(k_2)\rangle=ie\left[\langle\psi_1(k_2)\bar\psi_b(k_2)\rangle-\langle\psi_1(k_1)\bar\psi_b(k_1)\rangle\right]$$

左式为$(k_2-k_1)_\mu\mathbf S(k_2)\mathbf V^\mu(k_2,k_1)\mathbf S(k_1)$，右式为$ie\left[\mathbf S(k_2)-\mathbf S(k_1)\right]$，所以

$$(k_2-k_1)_\mu\mathbf V^\mu(k_2,k_1)=ie\left[\mathbf S(k_1)^{-1}-\mathbf S(k_2)^{-1}\right]$$

---

若$y=z$，则

$$-i\partial_\mu\langle T j^\mu(x)\psi_a(y)\bar\psi_b(y)\rangle=0\Rightarrow \partial_\mu\langle Tj^\mu(x)j^\nu(y)\rangle=0\Rightarrow k_\mu\Pi^{\mu\nu}(k)=0$$